1563. Послать таблицу
Джимми
необходимо вычислить функцию f(x, y),
где x и y целые числа в промежутке от 1 до n. Если ему известно f(x, y),
то он легко может найти f(k*x,
k*y),
где k – любое целое число, выполнив
простейшие вычисления над f(x, y)
и k.
Отметим, что
функция f не симметрична, поэтому значение f(x, y) не может быть получено из f(y, x).
Например, если n = 4, то Джимми изначально достаточно
знать 11 из 16 возможных входных комбинаций:

Остальные 5 значений он может без труда вычислить из уже имеющихся:
·
f(2, 2), f(3, 3) и f(4, 4) из f(1, 1);
·
f(2, 4) из f(1, 2);
·
f(4, 2) из f(2, 1);
Вход. Состоит из не более чем 600 строк.
Каждая строка содержит одно целое число n (1 ≤ n ≤ 50000). Последняя
строка содержит ноль и не обрабатывается.
Выход. Для
каждого входного значения n в
отдельной строке вывести минимальное количество значений функций, которое
следует знать Джимми для вычисления всех n2
значений f(x,
y).
|
Пример входа |
Пример выхода |
245
0 |
311
19 |
РЕШЕНИЕ
теория
чисел - функция Эйлера
Анализ алгоритма
Обозначим через
res(i) минимальное требуемое
количество известных значений f(x, y),
где x, y Î {1, …, i}. Очевидно, что res(1) = 1, так как при n = 1 достаточно знать f(1, 1).
Пусть известно
значение res(i). Для n = i
+ 1 следует найти значения
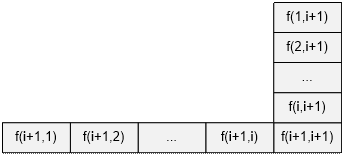
Значения f(j, i + 1) и f(i + 1, j), j Î {1, …, i + 1}, можно вычислить из известных
значений, если НОД(j, i + 1) > 1, то есть если числа j и i
+ 1 не являются взаимно простыми. Следовательно, необходимо знать все такие f(j, i + 1) и f(i + 1, j), для которых j и i + 1 взаимно простые. Число таких
значений равно 2 * j(i + 1), где j – функция Эйлера. Таким образом
res(1) =
1,
res(i + 1) = res(i) + 2 * j(i + 1), i > 1
Пример
Вычислим
значения res(i) для некоторых
начальных значений i:
res(1) =
1,
res(2) =
res(1) + 2 * j(2) = 1 + 2 * 1 = 3,
res(3) =
res(2) + 2 * j(3) = 3 + 2 * 2 = 7,
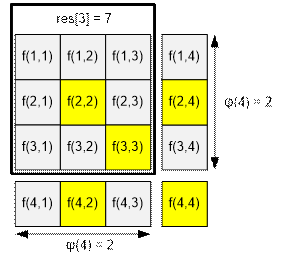
res(4) =
res(3) + 2 * j(4) = 7 + 2 * 2 = 11
Реализация алгоритма
Элементы массива
f[i] длины MAX = 50001 будут
содержать значения j(i). В ячейках res[i] будет храниться минимальное требуемое количество известных значений
f(x, y).
#define MAX 50001
int f[MAX], res[MAX];
Функция fi вычисляет
значение функции Эйлера j(n).
int
fi(int n)
{
int i, result
= n;
for(i = 2; i
<= sqrt(n); i++)
{
if (n % i
== 0) result -= result / i;
while (n %
i == 0) n /= i;
}
if (n > 1)
result -= result / n;
return
result;
}
Основная часть
программы. Находим все значения j(n), заносим их в массив f.
f[1] = 0;
for(i = 2; i < MAX; i++) f[i] =
fi(i);
Полагаем res[1]
= 1 и рекурсивно пересчитываем значения res[i].
res[1] = 1;
for(i = 2; i < MAX; i++) res[i] =
res[i-1] + 2 * f[i];
Для каждого
входного значения n выводим результат
res[n].
while(scanf("%d",&n),n)
printf("%d\n",res[n]);
Java реализация
import java.util.Scanner;
public class Main
{
static int MAX = 50001;
static int fi(int n)
{
int result = n;
for(int i = 2 ; i <= Math.sqrt(n);i++)
{
if (n % i == 0) result -= result / i;
while (n % i == 0) n /= i;
}
if (n > 1) result -= result / n;
return result;
}
public static void main(String[] args)
{
Scanner con = new Scanner(System.in);
int f[] = new int[MAX];
int res[] = new int[MAX];
f[1] = 0;
for(int i = 2; i < MAX; i++)
f[i] = fi(i);
res[1] = 1;
for(int i = 2; i < MAX; i++)
res[i] = res[i-1] + 2 * f[i];
while(con.hasNext())
{
int n = con.nextInt();
if (n == 0) break;
System.out.println(res[n]);
}
con.close();
}
}